State of art the competing risks survival analysis for cancer patients

Introduction

In some medical studies, the outcomes may occur by several potential causes. For example, in patients with colorectal cancer (CRC), there are at least two ways a patient would experience death outcome; experiencing death by colon cancer or by rectal cancer. In the simplest form of competing risks problem, there are two latent failure times (say T₁ and T₂) which only one of them [i.e., the minimum failure time (X = min)] could be observed along with an indicator of failure cause (1). Therefore, occurrence the outcome by one cause prevents the other cause(s) or makes them unobservable or un-interpretable (2).

Gail [1975] or Prentice et al. [1978] and Taşdelen et al. [2009] assessed the history and a variety of procedures for analysis of survival data in the presence of competing risks (3-5). Although the effect size of interest is dependent on the clinical question (6), but in many situations, the main focus is on marginal survival probability or marginal hazard rate for each cause. This means that eliminating or adjusting for other causes, the cause of interest how affects the outcome. For example, by considering the deaths caused by colon cancer, what is the probability of occurring death caused by rectal cancer?

Since there are correlations among outcomes occurring by the causes, marginal survival probability or marginal hazard rate would not be estimable without applying additional assumptions on the correlation structure of the failure times (7). Marginal survival probability or marginal hazard rate are equal to the marginal ones, only when the assumption of independence of failure times is satisfied (2). It is popular (and easier) to estimate cause-specific survival probability or hazard rate for the cause of interest considering as censored the outcomes by other causes. For example the survival probability or hazard rate for colon cancer is estimated considering the independent of death or censoring in colon and rectal cancer. The results obtained by the analyses which ignore this assumption produce biased estimations (8,9) considering the accuracy and precision of the estimates (10). In the other hand, this assumption can’t be checked by data itself and only a sensitivity analysis could be performed (2).

Various ways could be used to relax the problem of independence assumption in the competing risks survival analysis (11). As one of useful procedures, utilizing frailty models taking into account the correlation as a frailty component in the model will do a correction on model (10).

Adjusting the classic competing risks models using frailty

Finkelstein and Esaulova [2008], in addressing the problem of bivariate frailty competing risks model showed that by assuming dependent risks via a bivariate frailty (U₁, U₂), when the components of the system are conditionally on independent U₁ and U₂ are independent, then the mixture failure rate of the system can be constructed by the sum of mixture failure rate of individual components (11).

After applying the findings of Finkelstein and Esaulova [2008], survival times would be independent. In our study, we further use this idea to model competing risks by including frailty terms in the model. We constructed the likelihood function for the data by making use of Gamma frailty and applying the frailty distribution into the likelihood and taking integral with respect to u we have:

By taking the logarithm from equation above and summing over k competing events, the marginal log likelihood Klein [1992] is as follow (12):

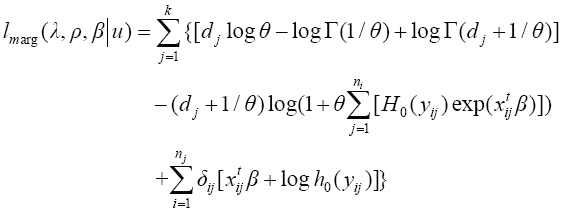
Based on this function, the effect of covariates was considered in the likelihood function and the parameters of interest were estimated along with their standard error (SE).

Addressing the findings on examples of colorectal cancer data

In this section, the findings of the method are addressed by a real data set on colorectal cancer. The findings have been published elsewhere (10) (and they are used as example here); however a brief introduction is followed.

Data were gathered in cancer registry center of Research Center of Gastroenterology and Liver Disease (RCGLD), Shahid Beheshti Medical University, Tehran, Iran. All patients with CRC diagnosis according to the pathology report of cancer registry were eligible for this study. A total of 1,219 patients [802 (65.8%) with colon cancer, 392 (32.2%) with rectal cancer] were entered in the study. The follow up time was defined as 1^st January 2002 (the date of diagnosis) up to the 1^st October 2007 as the time of the death from the disease or survival (censoring). Deaths were confirmed through the telephonic contact to relatives of patients.

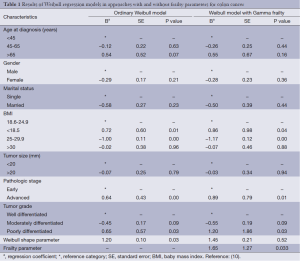
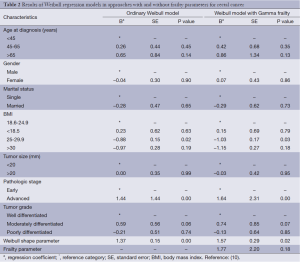
For all patients, the demographic and clinico-pathological characteristics (Table 1), were used in the analysis. Based on site topography of the cancer, colon and rectal cancers were considered as competing risks of death. The hazard of the colon and rectal cancers was computed by the Weibull regression with Gamma frailty to adjustment for the problem of independence assumption. Additionally the Weibull regression model without Gamma frailty was also fitted on the data. All analyses have been conducted using STATA 10 statistical software and a fixed value (=1) for Weibull scale parameter considered.

Table 1 Results of Weibull regression models in approaches with and without frailty parameters for colon cancer
Full table

Results

For colon cancer (Table 1), the frailty parameter was significant (parameter estimate =1.65, SE =1.27 and P value =0.033), therefore a significant heterogeneity existed which was caused by the dependence of the two competing risks. Although for rectal cancer (Table 2), the frailty parameter wasn’t significant (parameter estimate =1.77, SE =2.20 and P value =0.180), however a suggestive effect was observed (0.77 deviates from 1) and this amount substantially affect the parameter estimate and their SE’s.

Table 2 Results of Weibull regression models in approaches with and without frailty parameters for rectal cancer
Full table

In the second to fourth columns of Tables 1,2, the results (including regression coefficients, SE’s and P values) of ordinary regression are shown which were based on independence assumption of the survival times of patients with colon and rectal cancers. This assumption couldn’t be checked in this data, so there may be some uncertainty (bias and incorrect SE) in these results. In the following columns of tables, the results of Weibull model with gamma frailty are shown. In this approach, both the parameter estimates and their SE’s have been adjusted for model misspecifications.

Conclusions

In this study, the problem of not taking into consideration the independence in competing risks were addressed by using Weibull distribution for competing risks by introducing Gamma frailty in the models. The results were investigated using examples on a colorectal cancer data set. The findings showed a substantial adjustment for model (including regression coefficients and Weibul Shape parameter) by frailty component. The dependency of the risks not only affect the variance of the parameter estimates but also affects the parameter value itself (8). In the frailty approach, both the parameter estimates and their SE’s have been adjusted for model misspecifications. Therefore frailty model will adjust model on both aspects of accuracy and precision. This finding may be useful for many situations at which there is uncertainty about or the independence assumption of failure times is not hold, such as competing risks, recurrent events (13), clustered data (14) multicenter clinical trials (15). Like some other studies (14), as one of limitations of this study, only one distribution has been used frailty variable in this study. However, other distributions such as Log-Normal, Log-Logistic, Gompertz and Generalized Gamma are also recommended. Additionally only Gamma distribution has been used for frailty variable which has been suggested as suitable distribution (16). But other distributions could be recommended. Also this framework could be shift and addressed by Bayesian framework (17).

Acknowledgements

Disclosure: The authors declare no conflict of interest.

References

1. Klein JP, Bajorunaite R. Inference for competing risks, In: Advances in survival analysis, Handbook of statistics (V. 23). Amsterdam: Elsevier, 2004:291-311.
2. Klein JP, Moeschberger ML. Survival Analysis: techniques for Censored and truncated Data. second ed. New York: Springer, 2003.
3. Gail M. A review and critique of some models used in competing risk analysis. Biometrics 1975;31:209-22. [PubMed]
4. Prentice RL, Kalbfleisch JD, Peterson AV Jr, et al. The analysis of failure times in the presence of competing risks. Biometrics 1978;34:541-54. [PubMed]
5. Taşdelen B, Erdoğan S, Çağlikülekçi M, et al. Survival Analysis In The Presence Of Competing Risks. Journal of Biostatistics 2009;1:1-6.
6. Korn EL, Dorey FJ. Applications of crude incidence curves. Stat Med 1992;11:813-29. [PubMed]
7. Peterson AV. Bounds for a joint distribution function with fixed sub-distribution functions: Application to competing risks. Proc Natl Acad Sci U S A 1976;73:11-3. [PubMed]
8. Klein JP, Andersen PK. Regression modeling of competing risks data based on pseudovalues of the cumulative incidence function. Biometrics 2005;61:223-9. [PubMed]
9. Klein JP, Moeschberger ML. Independent or dependent competing risks: does it make a difference. Commun Stat Simul 1987;16:507-33.
10. Asghari-Jafarabadi M, Hajizadeh E, Kazemnejad A, et al. Overcoming the Problem of Independence Assumption in Competing Risks Model by Gamma Frailty Models: Application for Iranian Colorectal Cancer Patients. JP J Biostat 2010;4:123-38.
11. Finkelstein MS, Esaulova V. On asymptotic failure rates in bivariate frailty competing risks models. Stat Probab Lett 2008;78:1174-80.
12. Klein JP. Semiparametric estimation of random effects using the Cox model based on the EM algorithm. Biometrics 1992;48:795-806. [PubMed]
13. Cai J, Schaubel DE. Analysis of Recurrent Event Data. In Advances in survival analysis, Handbook of statistics (V. 23). Amsterdam: Elsevier, 2003:603-23.
14. Sahu SK, Dey DK. A comparison of frailty and other models for bivariate survival data. Lifetime Data Anal 2000;6:207-28. [PubMed]
15. Glidden DV, Vittinghoff E. Modelling clustered survival data from multicentre clinical trials. Stat Med 2004;23:369-88. [PubMed]
16. Hsu L, Gorfine M, Malone K. On robustness of marginal regression coefficient estimates and hazard functions in multivariate survival analysis of family data when the frailty distribution is mis-specified. Stat Med 2007;26:4657-78. [PubMed]
17. Asghari-Jafarabadi M. Frailty Competing Risks Model with Covariates for Survival Evaluation of Patients with Colorectal Cancer, Ph D Thesis. Tehran: Tarbiat Modares University, 2010.