Cure models in analyzing long-term survivors
Original Article

Cure models in analyzing long-term survivors

Mitra Rahimzadeh1, Behrooz Kavehie2, Mohammad Reza Zali3

1Research Center for Social Determinations of Health, Alborz University of Medical Sciences, Karaj, Iran; 2National Organization for Educational Testing (NOET), Tehran, Iran; 3Gastroenterology and Liver diseases Research Center, Shahid Beheshti University of Medical Sciences, Tehran, Iran

Correspondence to: Behrooz Kavehie, Ph.D. National Organization for Educational Testing (NOET), Tehran, Iran. Email: kavehiebehrooz@yahoo.com.

Introduction: If in the process of surviving data analysis, we are confronted with a high percentage of censors, caused when the study comes to an end, and if the time of survey is long enough, some percentage of the population might have long-term survival, as a result of which we are to make careful use of cure models. These models are categorized based on mixture and non-mixture cure models. Following the publication of Chen [1999] article and the submission of a procedure based on latent variable distribution in recent years, non-mixture or promotion time cure model have come to attention.

Purpose: In this article, Poisson and compound Poisson models are considered for latent variable distribution based on which the cure rate is estimated.

Methods: Model parameters were estimated using Bayesian approach, and to compare the models fitness, Deviance Information Criteria (DIC) was used. The applicability of the model has been shown on some stomach cancer data.

Conclusions: According to DIC, Poisson and compound Poisson cure models had a better fitting in comparison with the typical Weibull survival model.

Keywords: Bayesian approach; compound Poisson; cure model; long-term survival

Submitted Jul 15, 2014. Accepted for publication Aug 30, 2014.

doi: 10.3978/j.issn.2224-4778.2014.09.02

Introduction

In typical survival analysis, it is presupposed that all subjects are in expose to occurrence of the event. The longer the time of study, the higher an event is probable to approach one. However, practically, because of medical and early diagnose of cancers, a considerable percent of subjects survive as the population survives. In this kind of data, according to the presence of people with long-term survival (cured), making use of cured models is proposed.

Mixture cure model

This model was first presented by Boag and expanded by other writers including Farwell, Kuk and Chen, Sy and Taylor, Maller and Zhou, Peng and Dear (1-6). In this model, it is supposed that subjects are divided into two groups: first the percentage of those (θ) not affected by the event (cured) which can be survived by the probability of one, and the other percentage (1-θ) consists of those subjects affected by the given circumstance, and those which can be survived by one of the typical survival function. Population survival function can be reached by the following formula,

[1]

The Logistic Link function is most commonly used to obtain the percentage of the cured members (θ).

The second cure model known as non-mixture, promotion time cure models, or alternatively, as bounded cumulative hazard model—was first presented by Yakovlev and Tsodikov and was expanded by Chen (7,8).

Non-mixture cure model

In this model, it is supposed that the survival function for population equals where in which the covariates effect could be obtained on the cure rate and F(t) signifies cumulative distribution function. In his article, Chen made used of latent variable scheme in which N has Poisson distribution with θ parameter, signifying cancer cells which in the time of composes the detectable tumor and is considered to have F(t) distribution independent of N. As a result, the random variable T defined as has the survival function of and for , with the probability of , has survival probability of one.

It should be noted that the presented models in the cured model, if there are not any other cure subjects, are returnable to the typical survival models.

In recent years, different distribution is considered for the latent variable N. For instance, if we consider that the distribution of latent variable (N) is a Bernoulli, the mixture cure model is obtained. Accordingly, Cooner considered Geometric, Bernoulli and Binominal distributions; Borges et al. generalized power series distribution, Rodrigues et al. Conway-Maxwell Poisson (COM-Poisson) distribution and Rahimzadeh et al. Hyper Geometric Generalized Negative Binomial in the promotion time cure model (9-12).

It needs to be mentioned that the distribution of latent variable can be any divided distribution with the possibility of zero (in order to define curability proportion). In analyzing the long term survivors, another problem, besides the issue of over-dispersion, is that of skew. This is an added reason why the distributions in the process of problem solving should be different.

In this article, a model is presented in which the distribution of latent variable is considered as the compound Poisson, and to estimate the model parameters in Bayesian approach for model parameters, the Prior Distribution is considered. Depending on the Markov Chain Monte Carlo with Posterior distributions, model parameters are estimated. To select the best model based on Deviance Information Criteria (DIC), a model with the least DIC is chosen.

Methods

In Poisson distribution, mean and variance are equal. As compound Poisson distribution is to some extents the Poisson distribution, it has a separate parameter to define variance. Therefore, it is more flexible than the Poisson distribution.

In the model presented by Chen, Tsodikov et al. (13) showed that the population survival function can be obtained as follows:

[2]

In the function above, is the generating probability function of the latent variable N (the remaining cancer cells after cure). If N has the Poisson distribution with distribution function , the generating possibility function will be . Therefore, the population survival function by replacing 2 will result in and the cure rate will be .

The cure model with compound Poisson:

If the random variable φ includes Poisson distribution with θ parameter, the random variable N is defined as follows:

[3]

in which τ1,τ2,.. are independent random variables with Gamma(ν,η) distribution. In this case, Feller showed that the random variable N has compound Poisson distribution with (θ,ν,η) parameters (14).

It will be obviously known that this distribution is composed of two pieces: discrete piece, a positive probability of being equal to 0 for obtaining cure rate, and continuous piece, including the continuous positive value. It is to mention that in the discrete piece which includes the percentage of cure rate. The generating probability function for this distribution equals in which by replacement in eq. [2], the population survival function is resulted:

[4]

in which S(t) stands for the survival function in the promotion of time that can be considered as one of the typical survival functions such as Weibull, Gamma, Log-Normal, or Exponential piecewise. Depending on the parameter’s domain, the effect of the covariate variables can be obtained both on the parameter’s θ, using exponential link function, or on survival function parameters, using exponential link function, Logestic, Probit, and so forth.

To analyze data, non-mixture cure rate model with Poisson distribution and compound Poisson distribution were employed. A Weibull distribution was proposed to promotion of time survival function in which the survival function is as follows:

This survival function is ascending for α ≥1 values and descending for α ≤1 values.

The credible interval was used to adjust the significant effect of covariate variables. In Bayesian approach, a credible interval is a probabilistic region around a posterior parameter and is similar in use to a confidence interval in frequentist approach.

To make the model identifiable, ν = η, as a result of which the latent variable N, containing remaining cancer cells after treatment, will have compound Poisson distribution with mean θ and variance .

For distribution parameters, the non-informative prior distributions are considered in a way that the likelihood functions, to estimate Bayesian parameters, has a dominated effect on posterior distributions. Not questioning the whole issue, we can assume that the prior distributions are independent of each other.

For regression coefficients, uniform non-informative distribution is presented as and for Weibull parameters α and λ according to their range, Normal and Gamma distributions are used respectively and for v parameters, Gamma distribution is used.

Due to the high complexity and dimension of distributions of the posterior, it is not possible to find an analytical way to calculate the posterior distribution of the model parameters. Therefore, the Markov Chain Monte Carlo methods for inference about the model parameters are used. For this reason, sequential sampling of the full conditional distributions of the parameters using the Metropolis-Hastings algorithm will be built (15).The limiting probability distribution of these chains is a proper approximation for the posterior distribution parameters.

We made the comparison based on a model in which typical parametric survival models (without a cure rate), using the Weibull survival function, are considered. To compare the models, DIC estimation was used. This scale has the complexity and fitness of the model without the technical problems related to the non-informative of the prior distributions. It is defined as 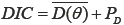in which 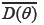represents the posterior deviation average along with fitness level. PD is defined as the number of effective parameters, showing the complexity of the model which equals the difference between the posterior mean of the deviance and the deviance of the posterior mean in model parameters, as to be represented by 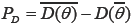. Based on these criteria, the model with the lowest DIC is the best. The criteria are useable for any sample size and be easily calculated by the Markov Chain Monte Carlo methods (16).

Results

Data used in this paper is part of the data gathered from the retrospective study in Taleghani hospital. In this study, a total of 746 patients during the years 2002 and 2006 referred to digest section of Taleghani hospital and received treatment. Also by reading out their phone calls and records, their health conditions were surveyed. This information includes the type of treatment, tumor size, stage of the disease and demographic information such as age and gender (17). In this paper, we consider those people who did not have surgical treatment and these included 291 patients. The average age of patients was 61.38±12.58 years, and 70.1% of the patients were men. In this period, 124 people died, 56% were still alive, or their survival status was unknown. About 11.3% of patients during diagnosis period were less than 45 years old. To analyze data, since data analysis in Bayesian approach cannot use case with missing values, the cases in which main factors were missing were omitted. As a result, for the final analysis only 192 patients remained.

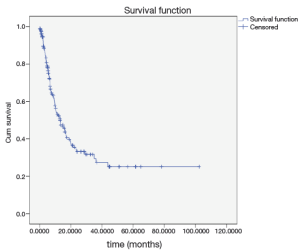
One of the easiest ways to identify long-term survival data is Kaplan-Meier survival graph. If the graph of survival before reaching the zero comes to a plateaus level following the years of exposure (Figure 1), this is the indicative of the presence of the cure rate. So to analyze this data, non-mixture cure model with a Poisson and compound Poisson distribution was used.

Figure 1 Kaplan-Meier survival function graph

Although more than half a century has passed since the advent of cure models, due to the complexity of these models, their application is not yet easily available. In STATA package there is a subprogram entitled CURREG by the help of which it is possible to fit the Bernoulli and Poisson promotion time cure models (18). Also a program is written in R package environment that enables fitting of cure models with nonparametric distribution like proportional hazard model (19). In the above mentioned programs, likelihood parameters are used to estimate parameters. As an alternative approach, Bayesian approach is used to estimate model parameters. To this end, packages such as WinBugs have provided a suitable environment to estimate model parameters using easy programming in Bayesian approach (20).The program used in this article is written in WinBugs package environment and was conducted by Bayesian estimation approach. To estimate model parameters in compound Poisson cure model, the following priors were used:

After producing samples to diagnosis the statistical convergence, Gelman–Rubin statistics was used to determine the proper burn-ins (21). Since the value of this statistic for all parameters is less than 1.8, 10,000 samples of the iterations seem to be appropriate. As a result, 100,000 samples were produced and a sample was recorded every ten iterations for reduction of auto correlation within chain. To compare the results of the cure model and typical survival models, typical survival model with Weibull function was fitted to this data.

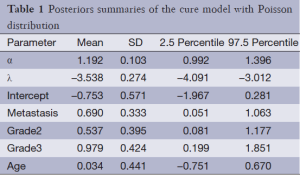
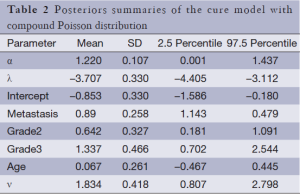
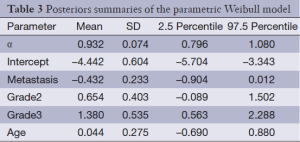
The results of fitting the models (compound Poisson and Poisson cure rate model and typical Weibull model) are presented in Tables 1-3. As can be seen in Tables 1-3, metastasis and stage of disease in all three models have a significant effect on the cure rate and survival function respectively, yet age has no significant effect. To compare these three models, the DIC criteria are shown in Table 4.

Table 1
Table 1 Posteriors summaries of the cure model with Poisson distribution
Full table
Table 2
Table 2 Posteriors summaries of the cure model with compound Poisson distribution
Full table
Table 3
Table 3 Posteriors summaries of the parametric Weibull model
Full table
Table 4
Table 4 Cure rate estimation based on the cure model with compound Poisson distribution
Full table

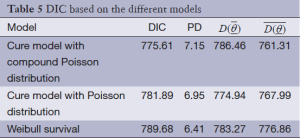
As shown in Table 4, the cure rate model with compound Poisson distribution with a DIC of 775.61 fits better than the Poisson cure rate model and the typical Weibull model with a deviation of 781.89 and 789.68. As the compound Poisson cure model was selected as the best model fitting to the data, the estimates of cure rates for this model are shown in Table 5. According to this table, we can see that the cure rate in metastasis patients is less than that in non-metastatic patients and the more advanced the stage rate is, the less cure rate will be.

Table 5
Table 5 DIC based on the different models
Full table

Discussion

Common models used in the analysis of survival data are very impressive. But in these models, the basic assumption is the occurrence of events happening with the increase of follow-up time. But for the analysis of survival data with long follow-up observation, some members are censored at the end of study; in this case, new models such as cure models are needed.

One advantage of these models besides estimating the cure rate is to reduce them to a common survival model in the absence of cure subjects. It is worth noting that the results of these models are reliable only if the study time is long enough. One of the easiest and most common ways to identify cure subjects is to draw Kaplan-Meier graph. If this graph before reaching zero comes to a plateau level (Figure 1), there would be evidence for the presence of cured members.

By comparing DIC criterion, it comes clear that both cure rate Poisson and compound Poisson models in comparison with the typical Weibull model had better fitting to the data.

In this study, the most important element causing reduction of cure rate was to metastasis cancer, which in many observations is known to be as the most influential element causing decrease in the survival of cancer patients. The other element was the stage of disease, which was categorized into three levels, and the cure rate decreased as the stage level increased. This finding was in coordination with results made from the other observations (22) while the age variable had no significant effect on cure rate.

Acknowledgements

Disclosure: The authors declare no conflict of interest.

References

  1. Boag JW. Maximum likelihood estimates of the proportion of patients cured by cancer therapy. J R Stat Soc B 1949;11:15-44.
  2. Farewell VT. The use of mixture models for the analysis of survival data with long-term survivors. Biometrics 1982;38:1041-6. [PubMed]
  3. Kuk AY, Chen HC. A mixture model combining logistic regression with proportional hazards regression. Biometrika 1992;79:531-41.
  4. Maller RA, Zhou S. eds. Survival Analysis with Long-Term Survivors. New York: Wiley, 1996.
  5. Sy JP, Taylor JM. Estimation in a Cox proportional hazards cure model. Biometrics 2000;56:227-36. [PubMed]
  6. Peng Y, Dear KB, Denham JW. A generalized F mixture model for cure rate estimation. Stat Med 1998;17:813-30. [PubMed]
  7. Yakovlev AY, Tsodikov AD. eds. Stochastic Models of Tumor Latency and Their Biostatistical Applications (Mathematical Biology and Medicine, Vol 1). World Scientific, 1996.
  8. Chen MH, Ibrahim JG, Sinha D. A new Bayesian model for survival data with a surviving fraction. J Am Stat Assoc 1999;94:909-19.
  9. Cooner F, Banerjee S, Carlin BP, et al. Flexible Cure Rate Modeling Under Latent Activation Schemes. J Am Stat Assoc 2007;102:560-72. [PubMed]
  10. Borges P, Rodrigues J, Balakrishnan N. Correlated destructive generalized power series cure rate models and associated inference with application to a cutaneous melanoma data. Comput Stat Data Anal 2012;56:1703-13.
  11. Rodrigues J, de Castro M, Cancho VG, et al. COM-Poisson cure rate survival models and an application to a cutaneous melanoma data. J Statist Plann Inference 2009;139:3605-11.
  12. Rahimzadeh M, Baghestani AR, Kavehei B. On hypergeometric generalized negative binomial distribution in promotion time cure model. J Stat Sci 2013;7:45-60.
  13. Tsodikov AD, Ibrahim JG, Yakovlev AY. Estimating cure rates from survival data: an alternative to two-component mixture models. J Am Stat Assoc 2003;98:1063-1078. [PubMed]
  14. Feller W. eds. An Introduction to Probability Theory and Its Applications, Vol. 2. New York: Wiley, 1971.
  15. Hastings WK. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970;57:97-109.
  16. Spiegelhalter DJ, Best NG, Carlin BP, et al. Bayesian measures of model complexity and fit (with discussion). J R Stat Soc B 2002;64:583-639.
  17. Pourhoseingholi MA, Moghimi-Dehkordi B, Safaee A, et al. Prognostic factors in gastric cancer using log-normal censored regression model. Indian J Med Res 2009;129:262-7. [PubMed]
  18. Buxton A. CUREREGR8: Stata module to estimate parametric cure regression (version 8.2). EconPapers 2013. Available online: http://econpapers.repec.org/software/bocbocode/s457734.htm
  19. Cai C, Zou Y, Peng Y, et al. Smcure: an R-package for estimating semiparametric mixture cure models. Comput Methods Programs Biomed 2012;108:1255-60. [PubMed]
  20. Spiegelhalter D, Thomas A, Best N, et al. WinBUGSUser Manual, Version 1.4. MRC Biostatistics Unit,Institute of Public Health and Department of Epidemi-ology and Public Health, Imperial College School of Medicine,UK,2003. Available online: http://www.mrc-bsu.cam.ac.uk/bugs
  21. Gelman A, Rubin DB. Markov chain Monte Carlo methods in biostatistics. Stat Methods Med Res 1996;5:339-55. [PubMed]
  22. Zhu HP, Xia X, Yu CH, et al. Application of Weibull model for survival of patients with gastric cancer. BMC Gastroenterol 2011;11:1. [PubMed]
Cite this article as: Rahimzadeh M, Kavehie B, Zali MR. Cure models in analyzing long-term survivors. Transl Gastrointest Cancer 2014;3(4):149-154. doi: 10.3978/j.issn.2224-4778.2014.09.02